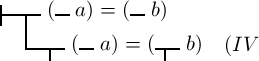§ 18. Wir wollen
nun mit lateinischen Buchstaben einige allgemeine Gesetze
aufstellen, von denen wir später Gebrauch machen müssen. Nach
§ 12 wäre
nur dann das Falsche, wenn Γ und Δ das Wahre
wären, während Γ nicht das Wahre
wäre. Dies ist unmöglich; also
Die ‚I‘ ist diesem Satze als Abzeichen (§ 14) gegeben, und so werden auch
fernerhin Abzeichen den Sätzen beigelegt werden. Wenn wir statt
‚b‘ ‚a‘ schreiben, können wir gleiche Unterglieder
verschmelzen, sodass wir in  einen besondern Fall von (I) haben, der auch ohne Erinnerung mit
unter (I) verstanden werden
soll. —Δ und
einen besondern Fall von (I) haben, der auch ohne Erinnerung mit
unter (I) verstanden werden
soll. —Δ und  sind immer verschieden und Wahrheitswerthe. Da nun —Γ ebenfalls immer ein Wahrheitswerth ist, so
muss er entweder mit —Δ oder mit
sind immer verschieden und Wahrheitswerthe. Da nun —Γ ebenfalls immer ein Wahrheitswerth ist, so
muss er entweder mit —Δ oder mit
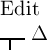 zusammenfallen. Daraus folgt, dass
zusammenfallen. Daraus folgt, dass 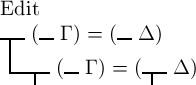 immer das Wahre ist; denn es würde nur dann das Falsche sein,
wenn
immer das Wahre ist; denn es würde nur dann das Falsche sein,
wenn 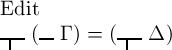 das
Wahre, d. h.
das
Wahre, d. h. 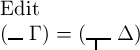 das Falsche, und (—Γ)=(—Δ) nicht das Wahre, d. h. das Falsche
wäre. Mit andern Worten:
das Falsche, und (—Γ)=(—Δ) nicht das Wahre, d. h. das Falsche
wäre. Mit andern Worten: 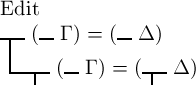 wäre nur dann das Falsche, wenn sowohl (—Γ)=(—Δ), als
auch
wäre nur dann das Falsche, wenn sowohl (—Γ)=(—Δ), als
auch  das
Falsche wäre, was, wie wir eben gesehen, nicht möglich ist. Also
Auf der rechten Seite des Gleichheitszeichens könnten die
Klammern allenfalls entbehrt werden. Aus der Bedeutung des Functionsnamens
\ξ (§ 11)
folgt
das
Falsche wäre, was, wie wir eben gesehen, nicht möglich ist. Also
Auf der rechten Seite des Gleichheitszeichens könnten die
Klammern allenfalls entbehrt werden. Aus der Bedeutung des Functionsnamens
\ξ (§ 11)
folgt
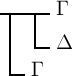
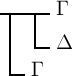
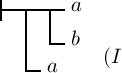
 einen besondern Fall von (I) haben, der auch ohne Erinnerung mit
unter (I) verstanden werden
soll. —Δ und
einen besondern Fall von (I) haben, der auch ohne Erinnerung mit
unter (I) verstanden werden
soll. —Δ und  sind immer verschieden und Wahrheitswerthe. Da nun —Γ ebenfalls immer ein Wahrheitswerth ist, so
muss er entweder mit —Δ oder mit
sind immer verschieden und Wahrheitswerthe. Da nun —Γ ebenfalls immer ein Wahrheitswerth ist, so
muss er entweder mit —Δ oder mit
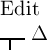 zusammenfallen. Daraus folgt, dass
zusammenfallen. Daraus folgt, dass 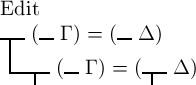 immer das Wahre ist; denn es würde nur dann das Falsche sein,
wenn
immer das Wahre ist; denn es würde nur dann das Falsche sein,
wenn 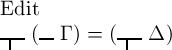 das
Wahre, d. h.
das
Wahre, d. h. 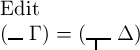 das Falsche, und (—Γ)=(—Δ) nicht das Wahre, d. h. das Falsche
wäre. Mit andern Worten:
das Falsche, und (—Γ)=(—Δ) nicht das Wahre, d. h. das Falsche
wäre. Mit andern Worten: 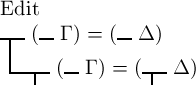 wäre nur dann das Falsche, wenn sowohl (—Γ)=(—Δ), als
auch
wäre nur dann das Falsche, wenn sowohl (—Γ)=(—Δ), als
auch  das
Falsche wäre, was, wie wir eben gesehen, nicht möglich ist. Also
das
Falsche wäre, was, wie wir eben gesehen, nicht möglich ist. Also