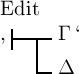
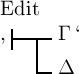 und
‚⊦Δ‘ kann geschlossen werden:
‚⊦Γ‘; denn, wäre Γ nicht das Wahre, so wäre, da Δ das Wahre ist,
und
‚⊦Δ‘ kann geschlossen werden:
‚⊦Γ‘; denn, wäre Γ nicht das Wahre, so wäre, da Δ das Wahre ist, 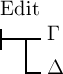 das
Falsche. Ich werde nun jedem in Begriffsschriftzeichen
aufgestellten Satze, wenn er später zu einer weitern
Beweisführung gebraucht werden soll, ein Abzeichen geben, um ihn heranziehen zu können.
Wenn nun so der Satz
das
Falsche. Ich werde nun jedem in Begriffsschriftzeichen
aufgestellten Satze, wenn er später zu einer weitern
Beweisführung gebraucht werden soll, ein Abzeichen geben, um ihn heranziehen zu können.
Wenn nun so der Satz 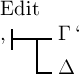 das Abzeichen ‚α‘ und ‚⊦Δ‘ das Abzeichen ‚β‘ erhalten hat, so schreibe ich den Schluss
entweder so
das Abzeichen ‚α‘ und ‚⊦Δ‘ das Abzeichen ‚β‘ erhalten hat, so schreibe ich den Schluss
entweder so
|
oder so |
|
|
und |
|
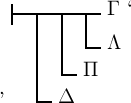 |
. |
|
oder |
|
| ‚ |
|
‘ | |