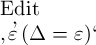
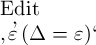mit
‚Δ‘ allgemein hätte aufrecht
erhalten lassen2,
so hätten wir in der Form 
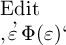einen Ersatz für den
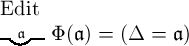das Wahre und mithin wäre auch 
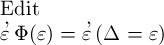das Wahre und zufolge unserer Gleichsetzung von 
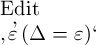und
‚Δ‘ wäre 
dasselbe wie Δ; d. h. in dem Falle,
dass Φ(ξ) ein Begriff ist, unter
den ein und nur ein Gegenstand fällt, bezeichnete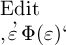 
diesen Gegenstand. Dies ist nun freilich nicht möglich, weil jene
Gleichsetzung in ihrer Allgemeinheit fallen gelassen werden
musste; aber wir können uns helfen, indem wir die Function
 |
 |
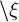das Argument ist, so sei der Werth der Function \ξ
Δ selbst;
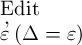das Argument ist, so sei das Argument selbst der Werth der
Function \ξ.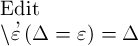
das
Wahre, und es bedeutet 
dann den unter den Begriff Φ(ξ)
fallenden Gegenstand, wenn Φ(ξ) ein
Begriff ist, unter den ein und nur ein Gegenstand fällt; in allen
andern Fällen bedeutet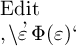 
dasselbe wie 
.
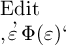So ist z. B.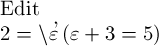 
das Wahre, weil 2 der einzige
Gegenstand ist, der unter den Begriff
das Wahre, weil unter den Begriff Quadratwurzel aus l nicht nur ein einziger
Gegenstand fällt. Es ist 
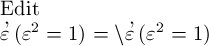das Wahre, weil unter den Begriff sich
selbst ungleich kein Gegenstand fällt. Es ist 
,
weil die Function ξ+3 kein Begriff
ist. Hierin haben wir einen Ersatz
für den bestimmten Artikel der Sprache, der dazu dient, aus
Begriffswörtern Eigennamen zu bilden. Wir bilden z. B. aus den
Worten
immer eine Bedeutung hat, mag nun die Function Φ(ξ) kein Begriff sein, oder ein Begriff, unter
den mehr als ein oder kein Gegenstand fällt, oder mag sie ein
Begriff sein, unter den ein und nur ein Gegenstand fällt.
2 Vergl. Anm. 1.
1 Ich nehme dabei als zugestanden an, dass es negative und irrationale Zahlen gebe.