§ 15. Etwas
weniger einfach ist folgende Schlussweise Ersetzung von - Schlussweisc - durch - Schlussweise -
[Fehlertyp: orth | Rev.: thiel]. Aus den beiden Sätzen
können wir auf den Satz 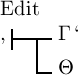 schliessen.
schliessen. 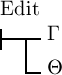 ist nämlich nur dann das Falsche, wenn Θ das Wahre und Γ
nicht das Wahre ist. Wenn aber Θ
das Wahre ist, so muss auch Δ das
Wahre sein, weil sonst
ist nämlich nur dann das Falsche, wenn Θ das Wahre und Γ
nicht das Wahre ist. Wenn aber Θ
das Wahre ist, so muss auch Δ das
Wahre sein, weil sonst 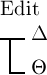 das Falsche wäre. Wenn aber Δ das
Wahre ist und Γ nicht das
Wahre
das Falsche wäre. Wenn aber Δ das
Wahre ist und Γ nicht das
Wahre
Seite 27
wäre, so wäre 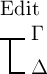 das
Falsche. Der Fall, wo
das
Falsche. Der Fall, wo 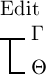 das Falsche wäre, findet also nicht statt und es ist
das Falsche wäre, findet also nicht statt und es ist 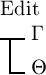 das
Wahre. Diesen Schluss schreibe ich
entweder so:
das
Wahre. Diesen Schluss schreibe ich
entweder so:
|
‚ |
|
‘ |
 |
|
oder so: |
|
‚ |
|
‘ |
 |
|
Wenn wir statt des Satzes (α) den in § 14 mit dem Abzeichen ‚γ‘ versehenen
als Praemisse haben, so müssen wir eigentlich wie dort erst eine
Umwandlung vor dem Schlusse vornehmen. Aber wir machen dies der
Kürze halber wie oben im Kopfe und schreiben
|
‚ |
|
‘ |
 |
|
oder |
|
‚ |
|
‘ |
 |
|
Es ist 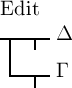 das
Falsche, wenn
das
Falsche, wenn 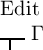 das Wahre und
das Wahre und 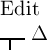 nicht das Wahre ist; d. h. wenn —Γ
das Falsche und Δ das Wahre ist. In
allen andern Fällen ist
nicht das Wahre ist; d. h. wenn —Γ
das Falsche und Δ das Wahre ist. In
allen andern Fällen ist 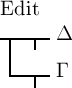 das Wahre. Dasselbe gilt aber auch von
das Wahre. Dasselbe gilt aber auch von 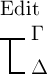 ,
sodass die Functionen
,
sodass die Functionen 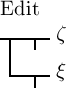 und
und 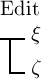 immer für dieselben Argumente denselben
Werth haben. Ebenso haben die Functionen
immer für dieselben Argumente denselben
Werth haben. Ebenso haben die Functionen 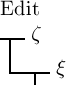 und
und
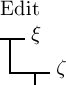 für
dieselben Argumente immer denselben Werth. Man führt diesen auf
den vorigen Fall zurück, indem man für ‚ζ‘
für
dieselben Argumente immer denselben Werth. Man führt diesen auf
den vorigen Fall zurück, indem man für ‚ζ‘ 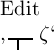 setzt und unmittelbar auf einander folgende Verneinungstriche
aufhebt. Auch die Functionen
setzt und unmittelbar auf einander folgende Verneinungstriche
aufhebt. Auch die Functionen 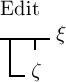 und
und 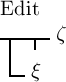 haben für dieselben Argumente immer denselben Werth. Wir können
also von dem Satze
haben für dieselben Argumente immer denselben Werth. Wir können
also von dem Satze 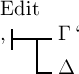 zu dem Satze
zu dem Satze 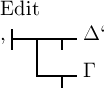 übergehen und umgekehrt von diesem zu jenem. Wir schreiben diese
Uebergänge so:
übergehen und umgekehrt von diesem zu jenem. Wir schreiben diese
Uebergänge so:
|
‚ |
|
‘ |
 |
|
und |
|
‚ |
|
‘ |
 |
|
Ebenso auch:
|
‚ |
|
‘ |
 |
|
und |
|
‚ |
|
‘ |
 |
|
Fälle, die auf den ersten zurückführbar sind durch
Aufhebung von Verneinungstrichen. Wir können dies in eine Regel
so fassen:
- Man darf ein Unterglied mit dem
Obergliede vertauschen, wenn man gleichzeitig die
Wahrheitswerthe beider umkehrt.
Wir nennen diesen Uebergang Wendung. Es können aber auch mehre
Seite 28
Unterglieder vorhanden sein. So haben wir
den Uebergang
|
‚ |
|
‘ |
 |
Indem wir von der Vertauschbarkeit der Unterglieder
stillschweigend Gebrauch machen, können wir aber auch schreiben:
|
‚ |
|
‘ |
 |
Durch zweimalige Wendung gelingt es, alle Unterglieder in
eins zusammenzufassen, wie folgt:
|
‚ |
|
‘ |
.  |
Wir fassen nämlich bei der zweiten
Wendung
als Oberglied und 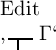 als Unterglied auf. Nennen wir zur Abkürzung den Wahrheitswerth
‚Θ‘! Der vorletzte Satz
geht dann über in
als Unterglied auf. Nennen wir zur Abkürzung den Wahrheitswerth
‚Θ‘! Der vorletzte Satz
geht dann über in 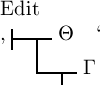 ,
woraus folgt
,
woraus folgt 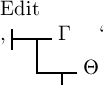 .
Setzen wir dann für ‚Θ‘ den
ausführlichen Ausdruck wieder ein, so erhalten wir den
Schlusssatz. Wie aus dem § 12 zu
ersehen ist, haben wir in
den Wahrheitswerth davon, dass Δ das Wahre, Λ
nicht das Wahre und Π das Wahre
sei. Nehmen wir die Sätze
als gegeben an, so können wir so folgern: wir fassen
zunächst die Unterglieder von (ε) zusammen:
.
Setzen wir dann für ‚Θ‘ den
ausführlichen Ausdruck wieder ein, so erhalten wir den
Schlusssatz. Wie aus dem § 12 zu
ersehen ist, haben wir in
den Wahrheitswerth davon, dass Δ das Wahre, Λ
nicht das Wahre und Π das Wahre
sei. Nehmen wir die Sätze
als gegeben an, so können wir so folgern: wir fassen
zunächst die Unterglieder von (ε) zusammen:
|
‚ |
|
‘ |
 |
Dies können wir dadurch vereinfachen, dass wir
‚Δ‘ nur einmal schreiben:
|
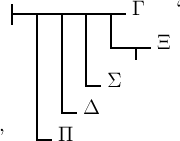 |
|
;  |
denn
ist immer derselbe Wahrheitswerth wie 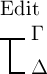 .
.
- Ein zweimal auftretendes
Unterglied braucht nur einmal geschrieben zu werden.
Wir nennen dies die Verschmelzung gleicher
Unterglieder. Ich schreibe nun
diesen Uebergang abgekürzt so:
|
‚ |
|
‘ |
 |
|
oder so: |
|
‚ |
|
‘ |
 |
|
und stelle für ihn folgende Regel auf:
- Wenn
dieselbe Zeichenverbindung in einem Satze als Oberglied und in
einem andern als Unterglied auftritt, so kann man auf einen
Satz schliessen, in welchem das Oberglied des zweiten als
Oberglied und alle Unterglieder beider ohne das genannte als
Unterglieder erscheinen. Ersetzung von - erscheinen - durch - erscheinen. -
[Fehlertyp: interp] Doch
brauchen Unterglieder, die in beiden vorkommen, nur einmal
geschrieben zu werden.
In ähnlicher Weise wie in
§ 14 können wir hier zwei
Schlüsse zusammenziehen. Es seien z. B. ausser (ε) die Sätze
gegeben, so können wir schreiben
Seite 30
|
‚ |
|
‘ |
 |
|
und |
|
‚ |
|
‘ |
 |
|
|
1 Wir können jetzt wie im Anfange
dieses Paragraphen schliessen, da dieser Satz dieselbe Form hat
wie dort (δ).
2 Wir lösen jetzt das zusammengesetzte
Unterglied wieder auf.
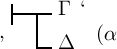
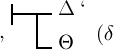
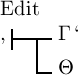 schliessen.
schliessen. 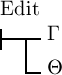 ist nämlich nur dann das Falsche, wenn Θ das Wahre und Γ
nicht das Wahre ist. Wenn aber Θ
das Wahre ist, so muss auch Δ das
Wahre sein, weil sonst
ist nämlich nur dann das Falsche, wenn Θ das Wahre und Γ
nicht das Wahre ist. Wenn aber Θ
das Wahre ist, so muss auch Δ das
Wahre sein, weil sonst 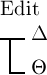 das Falsche wäre. Wenn aber Δ das
Wahre ist und Γ nicht das
Wahre
das Falsche wäre. Wenn aber Δ das
Wahre ist und Γ nicht das
Wahre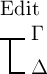 das
Falsche. Der Fall, wo
das
Falsche. Der Fall, wo 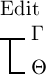 das Falsche wäre, findet also nicht statt und es ist
das Falsche wäre, findet also nicht statt und es ist 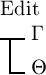 das
Wahre. Diesen Schluss schreibe ich
entweder so:
das
Wahre. Diesen Schluss schreibe ich
entweder so:
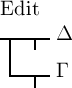 das
Falsche, wenn
das
Falsche, wenn 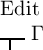 das Wahre und
das Wahre und 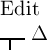 nicht das Wahre ist; d. h. wenn —Γ
das Falsche und Δ das Wahre ist. In
allen andern Fällen ist
nicht das Wahre ist; d. h. wenn —Γ
das Falsche und Δ das Wahre ist. In
allen andern Fällen ist 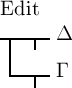 das Wahre. Dasselbe gilt aber auch von
das Wahre. Dasselbe gilt aber auch von 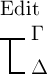 ,
sodass die Functionen
,
sodass die Functionen 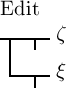 und
und 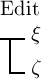 immer für dieselben Argumente denselben
Werth haben. Ebenso haben die Functionen
immer für dieselben Argumente denselben
Werth haben. Ebenso haben die Functionen 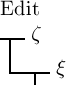 und
und
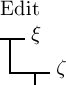 für
dieselben Argumente immer denselben Werth. Man führt diesen auf
den vorigen Fall zurück, indem man für ‚ζ‘
für
dieselben Argumente immer denselben Werth. Man führt diesen auf
den vorigen Fall zurück, indem man für ‚ζ‘ 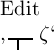 setzt und unmittelbar auf einander folgende Verneinungstriche
aufhebt. Auch die Functionen
setzt und unmittelbar auf einander folgende Verneinungstriche
aufhebt. Auch die Functionen 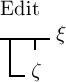 und
und 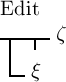 haben für dieselben Argumente immer denselben Werth. Wir können
also von dem Satze
haben für dieselben Argumente immer denselben Werth. Wir können
also von dem Satze 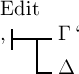 zu dem Satze
zu dem Satze 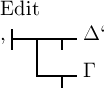 übergehen und umgekehrt von diesem zu jenem. Wir schreiben diese
Uebergänge so:
übergehen und umgekehrt von diesem zu jenem. Wir schreiben diese
Uebergänge so:
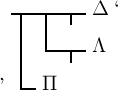
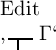 als Unterglied auf. Nennen wir zur Abkürzung den Wahrheitswerth
als Unterglied auf. Nennen wir zur Abkürzung den Wahrheitswerth
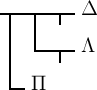
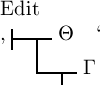 ,
woraus folgt
,
woraus folgt 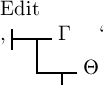 .
Setzen wir dann für ‚Θ‘ den
ausführlichen Ausdruck wieder ein, so erhalten wir den
Schlusssatz. Wie aus dem § 12 zu
ersehen ist, haben wir in
.
Setzen wir dann für ‚Θ‘ den
ausführlichen Ausdruck wieder ein, so erhalten wir den
Schlusssatz. Wie aus dem § 12 zu
ersehen ist, haben wir in
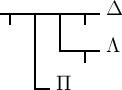

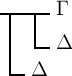
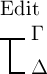 .
.