Kant: AA IV, Metaphysische Anfangsgründe ... , Seite 492
Zeile:
Text (Kant):
[ Seite 491 ] [ Seite 493 ] [ Inhaltsverzeichnis ]
Kant: AA IV, Metaphysische Anfangsgründe ... , Seite 492 |
|||||||
Zeile:
|
Text (Kant):
|
|
|
||||
| 01 | Dritter Fall, da zwei Bewegungen eben desselben Punkts nach | ||||||
| 02 | Richtungen, die einen Winkel einschließen, verbunden vorgestellt | ||||||
| 03 | werden. | ||||||
 |
|||||||
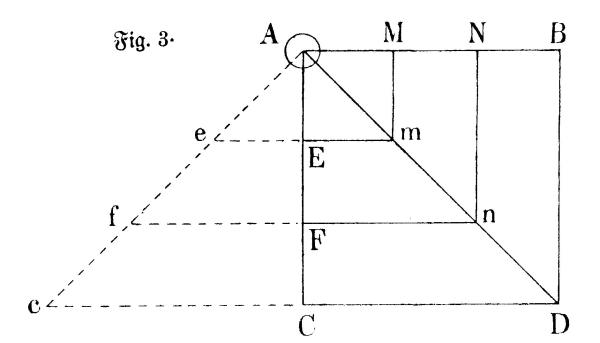
| 04 | Die zwei gegebenen Bewegungen sind AB und AC deren Geschwindigkeit | ||||||
| 05 | und Richtungen durch diese Linien, der Winkel aber, den die letztere | ||||||
| 06 | einschließen, durch BAC ausgedrückt wird (er mag wie hier ein rechter, | ||||||
| 07 | aber auch ein jeder beliebige schiefe Winkel sein). Wenn nun diese zwei | ||||||
| 08 | Bewegungen zugleich in den Richtungen AB und AC und zwar in einem | ||||||
| 09 | und demselben Raume geschehen sollen: so würden sie doch nicht in diesen | ||||||
| 10 | beiden Linien AB und AC zugleich geschehen können, sondern nur in | ||||||
| 11 | Linien, die diesen parallel laufen. Es würde also angenommen werden | ||||||
| 12 | müssen: daß eine dieser Bewegungen in der anderen eine Veränderung | ||||||
| 13 | (nämlich die Abbringung von der gegebenen Bahn) wirkte, wenn gleich | ||||||
| 14 | beiderseits Richtungen dieselbe blieben. Dieses ist aber der Voraussetzung | ||||||
| 15 | des Lehrsatzes zuwider, welche unter dem Worte Zusammensetzung andeutet: | ||||||
| 16 | daß beide gegebene Bewegungen in einer dritten enthalten, mithin | ||||||
| 17 | mit dieser einerlei seien, und nicht, daß, indem eine die andere verändert, | ||||||
| 18 | sie eine dritte hervorbringen. | ||||||
| 19 | Dagegen nehme man die Bewegung AC als im absoluten Raume | ||||||
| 20 | vor sich gehend an, anstatt der Bewegung AB aber die Bewegung des relativen | ||||||
| 21 | Raumes in entgegengesetzter Richtung. Die Linie AC sei in drei | ||||||
| 22 | gleiche Theile AE EF FC getheilt. Während daß nun der Körper A im | ||||||
| 23 | absoluten Raume die Linie AE durchläuft, durchläuft der relative Raum | ||||||
| 24 | und mit ihm der Punkt E den Raum Ee=MA ; während daß der Körper | ||||||
| 25 | die zwei Theile zusammen =AF durchläuft, beschreibt der relative | ||||||
| [ Seite 491 ] [ Seite 493 ] [ Inhaltsverzeichnis ] |
|||||||