Kant: AA IV, Metaphysische Anfangsgründe ... , Seite 491

      
           
 

Zeile:

 

Text (Kant):

 

Abbildung (Kant)

 

 

  
  01 Dagegen wenn der Körper A mit der Geschwindigkeit AB im absoluten      
  02 Raume als bewegt vorgestellt wird, und ich gebe überdem dem relativen      
  03 Raume eine Geschwindigkeit ab = AB in entgegengesetzter Richtung      
  04 ba = CB , so ist dieses eben dasselbe, als ob ich die letztere Geschwindigkeit      
  05 dem Körper in der Richtung AB ertheilt hätte (Grundsatz). Der      
  06 Körper bewegt sich aber alsdann in derselben Zeit durch die Summe der      
  07 Linien AB und BC=2ab , in welcher er die Linie ab=AB allein      
  08 würde zurückgelegt haben, und seine Geschwindigkeit ist doch als die      
  09 Summe der zwei gleichen Geschwindigkeiten AB und ab vorgestellt, welches      
  10 das ist, was verlangt wurde.      
           
  11 Zweiter Fall, da zwei Bewegungen in gerade entgegengesetzten      
  12 Richtungen an einem und demselben Punkte sollen verbunden      
  13 werden.      
           
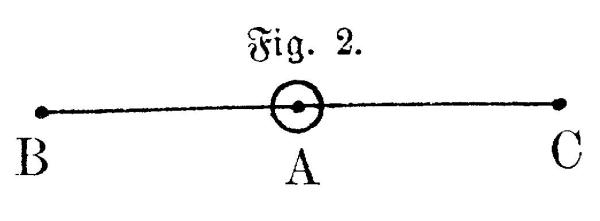
  14 Es sei AB die eine dieser Bewegungen und AC die andere in entgegengesetzter      
  15 Richtung, deren Geschwindigkeit Gerade; Anfangspunkt B; Endpunkt C; Mittelpunkt A, der mit Kreis versehen ist    
  16 wir hier der ersten gleich annehmen    
  17 wollen: so würde der Gedanke selbst, zwei    
  18 solche Bewegungen in einem und demselben    
  19 Raume an eben demselben Punkte als zugleich vorzustellen, mithin      
  20 der Fall einer solchen Zusammensetzung der Bewegungen selbst unmöglich      
  21 sein, welches der Voraussetzung zuwider ist.      
           
  22 Dagegen denket euch die Bewegung AB im absoluten Raume, statt      
  23 der Bewegung AC aber in demselben absoluten Raume die entgegengesetzte      
  24 CA des relativen Raumes mit eben derselben Geschwindigkeit, die      
  25 (nach Grundsatz) der Bewegung AC völlig gleich gilt und also gänzlich      
  26 an die Stelle derselben gesetzt werden kann: so lassen sich zwei gerade entgegengesetzte      
  27 und gleiche Bewegungen desselben Punkts zu gleicher Zeit      
  28 gar wohl darstellen. Weil nun der relative Raum mit derselben Geschwindigkeit      
  29 CA=AB in derselben Richtung mit dem Punkte A bewegt      
  30 ist, so verändert dieser Punkt oder der in ihm befindliche Körper in Ansehung      
  31 des relativen Raumes seinen Ort nicht, d. i. ein Körper, der nach      
  32 zwei einander gerade entgegengesetzten Richtungen mit gleicher Geschwindigkeit      
  33 bewegt wird, ruht, oder allgemein ausgedrückt: seine Bewegung ist      
  34 der Differenz der Geschwindigkeiten in der Richtung der größeren gleich      
  35 (welches sich aus dem Bewiesenen leicht folgern läßt).      
           
           
     

[ Seite 490 ] [ Seite 492 ] [ Inhaltsverzeichnis ]