Seite 42
§
25. Wir bedürfen noch einer Ausdrucksweise für die
Allgemeinheit hinsichtlich der Functionen zweiter Stufe mit einem
Argumente zweiter Art. Man könnte meinen, dass dies noch längst
nicht genügte; aber wir werden sehen, dass wir mit dieser
auskommen, und dass auch sie nur in einem einzigen Satze
vorkommt. Es mag hier zunächst nur kurz bemerkt werden, dass
diese Sparsamkeit dadurch möglich wird, dass die Functionen
zweiter Stufe in gewisser Weise durch Functionen erster Stufe
vertreten werden können, wobei die Functionen, die als Argumente
jener erscheinen, durch ihre Werthverläufe vertreten werden. Doch
die dazu nöthige Bezeichnungsweise gehört nicht zu den
ursprünglichen der Begriffsschrift; wir werden sie später mittels
unserer Urbezeichnungen Ersetzung
von - Urbezeichungen - durch - Urbezeichnungen - [Fehlertyp:
orth] einführen. Da unsere
Ausdrucksweise nur in einem einzigen Satze gebraucht wird, ist es
unnöthig, sie ganz allgemein zu erklären. Wir deuten eine Function zweiter Stufe mit
einem Argumente zweiter Art so an:
mittels des lateinischen
Functionsbuchstaben ‚M‘,
wie wir mit ‚f(ξ)‘ eine Function
erster Stufe mit einem Argumente andeuten. ‚φ( )‘ macht hier die Argumentstelle kenntlich,
wie ‚ξ‘ es in ‚f(ξ)‘ thut. Der Buchstabe ‚β‘ füllt hier in der Klammer die Stelle des
Arguments der als Argument auftretenden Function aus. Der
Gebrauch von ‚Mβ(φ(β))‘ ist für Functionen
zweiter Stufe ganz entsprechend dem von ‚f(ξ)‘ für Functionen erster Stufe. Wir
bedienen uns dieses Allgemeinheitsausdrucks in folgendem Gesetze
in Worten: Was von allen Functionen erster Stufe mit
einem Argumente gilt, das gilt auch von irgendeiner. Dies Gesetz
ist offenbar das für unsere Functionen zweiter Stufe, was
(IIa) für Functionen erster
Stufe ist. Dem Buchstaben ‚f‘ in
(IIa) entspricht hier
‚Mβ‘ dem ‚a‘ in (IIa)
entspricht hier ‚f‘ und dem
‚a‘ ‚f‘. Es sei Ωβ(φ(β)) eine Function zweiter
Stufe mit einem Argumente zweiter Art, dessen Stelle durch
‚φ‘ kenntlich gemacht ist. Dann ist
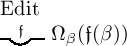 nur
dann das Wahre, wenn für jedes passende Argument der Werth
unserer Function zweiter Stufe das Wahre ist. Dann muss auch
Ωβ(Φ(β)) das Wahre sein. Mithin ist
immer das Wahre, was auch Φ(ξ) für eine Function erster Stufe mit einem
Argumente sein möge, einerlei ob
nur
dann das Wahre, wenn für jedes passende Argument der Werth
unserer Function zweiter Stufe das Wahre ist. Dann muss auch
Ωβ(Φ(β)) das Wahre sein. Mithin ist
immer das Wahre, was auch Φ(ξ) für eine Function erster Stufe mit einem
Argumente sein möge, einerlei ob 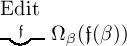 das
Wahre oder das Falsche ist; und das besagt unser Gesetz (IIb) allgemein für jede Function
zweiter Stufe mit einem Argumente zweiter Art.
das
Wahre oder das Falsche ist; und das besagt unser Gesetz (IIb) allgemein für jede Function
zweiter Stufe mit einem Argumente zweiter Art.
1 Dieser Buchstabe ist also kein
Gegenstandsbuchstabe.
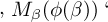
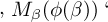

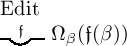 nur
dann das Wahre, wenn für jedes passende Argument der Werth
unserer Function zweiter Stufe das Wahre ist. Dann muss auch
Ωβ(Φ(β)) das Wahre sein. Mithin ist
nur
dann das Wahre, wenn für jedes passende Argument der Werth
unserer Function zweiter Stufe das Wahre ist. Dann muss auch
Ωβ(Φ(β)) das Wahre sein. Mithin ist

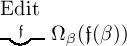 das
Wahre oder das Falsche ist; und das besagt unser Gesetz (IIb) allgemein für jede Function
zweiter Stufe mit einem Argumente zweiter Art.
das
Wahre oder das Falsche ist; und das besagt unser Gesetz (IIb) allgemein für jede Function
zweiter Stufe mit einem Argumente zweiter Art.