Kant: AA I, VIRO ILLUSTRISSIMO, GENEROSISSIMO ... , Seite 478
Zeile:
Text (Kant):
Abbildung (Kant)
[ Seite 477 ] [ Seite 479 ] [ Inhaltsverzeichnis ]
Kant: AA I, VIRO ILLUSTRISSIMO, GENEROSISSIMO ... , Seite 478 |
|||||||
Zeile:
|
Text (Kant):
|
Abbildung (Kant)
|
|
||||
| 01 | PROP. III THEOREMA. Spatium, quod corpora implent, est in | ||||||
| 02 | infinitum divisibile, neque igitur constat partibus primitivis atque simplicibus. | ||||||
| 03 | |||||||
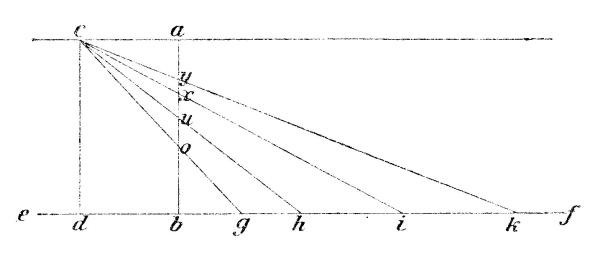
| 04 | Data linea ef indefinite producta, h.e. ita, ut ulterius semper pro lubitu | ||||||
| 05 | produci possit, alia ab physica, h.e. si ita arridet, partibus materiae primitivis | ||||||
| 06 | conflata, insistat ipsi |  |
|||||
| 07 | ad angulos rectos. Ad | ||||||
| 08 | latus alia erecta sit, | ||||||
| 09 | cd priori aequalis et | ||||||
| 10 | similiter posita, quod | ||||||
| 11 | fieri posse non solum | ||||||
| 12 | sensu geometrico, sed | ||||||
| 13 | et physico non infitiaberis. | ||||||
| 14 | Notentur in linea ef puncta quaelibet, g , h , i , k , et sic in indefinitum. | ||||||
| 15 | Primo nemo in dubium vocabit, inter duo quaevis puncta seu, si mavis, monades | ||||||
| 16 | datas, lineam rectam physicam duci posse. Sit itaque ducta cg et | ||||||
| 17 | locus, ubi haec intersecat perpendicularem ab erit o . Iam ducta concipiatur | ||||||
| 18 | alia linea physica inter puncta c et h , et erit locus u , ambabus lineis ch et ab | ||||||
| 19 | communis, puncto a propior. Sicque porro, ductis ex eodem puncto c ad | ||||||
| 20 | quaevis in linea ef in infinitum producta, puncta, i , k , cet., semper puncta | ||||||
| 21 | intersectionis, x , y cet. propinquiora fient puncto a , ut vel geometriae plane | ||||||
| 22 | ignaro per se liquet. Et si putas, lineas hasce physicas tandem iusto artiores | ||||||
| 23 | sibi contiguas fore, ut iuxta se consistere non possint, inferiores ductae auferri | ||||||
| 24 | possunt, et nihilo minus patet, loca intersectionis puncto a magis magisque | ||||||
| 25 | appropinquare debere*), prouti in linea indefinita ef longinquius atque longinquius | ||||||
| 26 | punctum notaveris. Quae vero longinquitas quia in infinitum prorogari | ||||||
| 27 | potest, appropinquatio etiam intersectionis versus punctum a infinitis incrementi | ||||||
| 28 | partibus augescere potest. Neque vero unquam intersectio hoc pacto in | ||||||
| 29 | punctum a cadet; quippe punctis c et a aequaliter distantibus a linea ef linea | ||||||
| 30 | puncta c et a iungens et, quousque libet, continuata semper tantundem distabit | ||||||
| 31 | a subiecta linea ef neque huic unquam occurrere potest, quod contra hypothesin. | ||||||
| 32 | Adeoque continua divisione lineae oa nunquam pervenitur ad partes primitivas | ||||||
| 33 | non ulterius dividendas, h. e. spatium est in infinitum divisibile, nec | ||||||
| 34 | constat partibus simplicibus. | ||||||
| 35 | SCHOLION. Demonstrationem hanc a permultis physicorum iam usurpatam | ||||||
| 36 | huc allegavi et quantum maxima fieri potuit perspicuitate ad physicum | ||||||
| 37 | spatium accomodavi, ne, qui generali de diversitate spatiorum geometrici et | ||||||
| *) Neque unquam puncta y et x coincidere possunt, quia alias lineae cy et cx aeque coinciderent, et coincideret linea ck lineae ci quod contra postulata. | |||||||
| [ Seite 477 ] [ Seite 479 ] [ Inhaltsverzeichnis ] |
|||||||