Kant: AA XIV, Mathematik , Seite 035
Zeile:
Text:
[ Seite 034 ] [ Seite 036 ] [ Inhaltsverzeichnis ]
Kant: AA XIV, Mathematik , Seite 035 |
|||||||
Zeile:
|
Text:
|
|
|
||||
| 01 |  |
||||||
| 02 | Links von der Figur: | ||||||
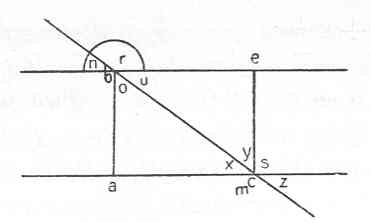
| 03 | (g be = ac, folglich alle drey Seiten des triangels bricht ab. ) | ||||||
| 04 | Rechts von der Figur: | ||||||
| (g | |||||||
| 04 | |||||||
| 05 | |||||||
| 06 | |||||||
| 07 | |||||||
| ) | |||||||
| 08 | Wenn nun die Perpendicularlinie ba auch bey b einen rechten winkel o + u | ||||||
| 09 | macht und die perpendicularlinie ce auch bey c den gleichen x + y macht, so ist | ||||||
| 10 | r + u = 2R, y + s + z = 2R. Nun ist o + u + x + y = r + u + y +s + z. | ||||||
| 11 | Also o + x = r + s + z. Aber z = y. Also o + x = r + s + y. Nun ist s = o + u, | ||||||
| 12 | also o + x = r + o + u + y, x = r + u + y. | ||||||
| 13 | |||||||
| 14 | |||||||
| 15 | |||||||
| 16 | |||||||
| [ Seite 034 ] [ Seite 036 ] [ Inhaltsverzeichnis ] |
|||||||