Kant: AA IX, Immanuel Kant's Logik Ein ... , Seite 126

		Kant: AA IX, Immanuel Kant's Logik Ein ... , Seite 126

	Zeile:	Text (Kant):
	01	vier Figuren bestimmt. Es bezeichne S das Subject der Conclusion, P das
	02	Prädicat derselben und M den terminum medium , so läßt sich das Schema
	03	für die gedachten vier Figuren in folgender Tafel darstellen:
	04



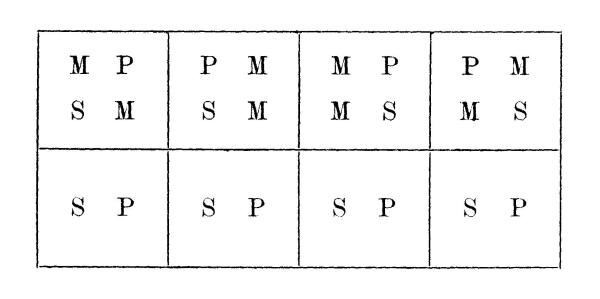	07	§. 69.
	08	Regel für die erste Figur, als die einzig gesetzmäßige.

	09	Die Regel der ersten Figur ist: daß der Major ein allgemeiner,
	10	der Minor ein bejahender Satz sei. Und da dieses die allgemeine
	11	Regel aller kategorischen Vernunftschlüsse überhaupt sein muß: so ergiebt
	12	sich hieraus, daß die erste Figur die einzig gesetzmäßige sei, die allen
	13	übrigen zum Grunde liegt, und worauf alle übrigen, sofern sie Gültigkeit
	14	haben sollen, durch Umkehrung der Prämissen ( metathesin praemissorum )
	15	zurückgeführt werden müssen.

	16	Anmerkung. Die erste Figur kann eine Conclusion von aller Quantität und
	17	Qualität haben. In den übrigen Figuren giebt es nur Conclusionen von gewisser
	18	Art; einige modi derselben sind hier ausgeschlossen. Dies zeigt schon
	19	an, daß diese Figuren nicht vollkommen, sondern daß gewisse Einschränkungen
	20	dabei vorhanden sind, die es verhindern, daß die Conclusion nicht in allen
	21	modis , wie in der ersten Figur, stattfinden kann.

	22	§. 70.
	23	Bedingung der Reduction der drei letztern Figuren auf die
	24	erstere.

	25	Die Bedingung der Gültigkeit der drei letztern Figuren, unter welcher
	26	in einer jeden derselben ein richtiger Modus des Schließens möglich ist,

		[ Seite 125 ] [ Seite 127 ] [ Inhaltsverzeichnis ]

§. 69.

Regel für die erste Figur, als die einzig gesetzmäßige.

§. 70.

Bedingung der Reduction der drei letztern Figuren auf die

erstere.