Kant: AA I, MEDITATIONUM QUARUNDAM DE IGNE ... , Seite 375

      
           
 

Zeile:

 

Text (Kant):

 

Abbildung (Kant)

 

 

  
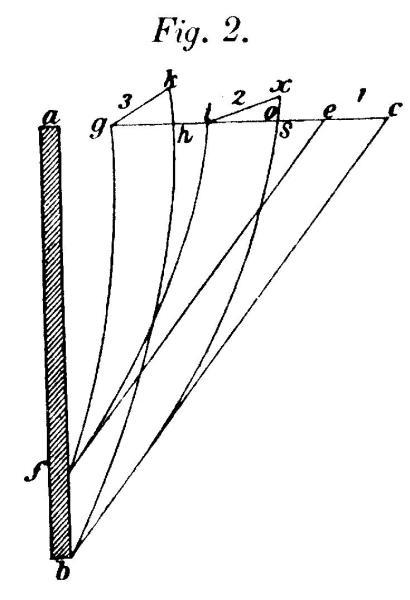
  01 Verum nunc, quanam ratione vires spatii compressionis comparatae se      
  02 habeant, indagandum. Margo xb in situ 2, quantumlibet aliquantulum incurvatus,      
  03 tamen in casu compressionum mediocrium pro recto haberi potest, item      
  04 linea kb in situ 3; ponatur porro, sectionem elastri Wie Fig.1. S.374; einziger Unterschied Gerade f nicht vorhanden    
  05 horizontalem ec no. 1 continuatam per puncta i et g    
  06 transire, quod, quoniam in mediocri compressionis gradu    
  07 quam proxime accidit, hic absque errore sumi poterit.    
  08 Est itaque in triangulo ixs angulus x = angulo c , quippe    
  09 eadem est sectio elastri, quae no. 1, angulus s aequatur    
  10 verticali suo o , ideoque triangula scb et ixs sunt    
  11 similia. Pariter in triangulo gkh no. 3 omnia cum    
  12 triangulo hcb eadem ratione se habent, ideoque argumentatio    
  13 sequens prodit:    
  14    ix : xs           = bc : sc    
  15 kh : gk (=ix) = hc bc    
  16 xs : kh          = sc hc      
  17 hoc est: quantitates xs et kh quibus distenditur elastri margo extimus bc sunt      
  18 in ratione spatiorum compressionis sc et hc .      
           
  19 Cum vero e prop. 4. constet, secundum hypothesin nostram vires      
  20 distendentes quantitati distensionis proportionales esse oportere, hoc in casu      
  21 liquet, vires elastrum comprimentes spatio compressionis proportionales fore.      
           
  22 Egregie asserta haec nostra, quae de la Hire in Monum. R. A. Sc. Paris.      
  23 anni 1705 circa compressionem elastrorum comperta prodidit, stabiliunt; si      
  24 rem sollicite examinaveris per aliam qualemcunque hypothesin vix tam apte      
  25 et congrue explicanda.      
           
  26
Corollarium generale.
     
           
  27 Omne itaque corpus, si recte sentio, partibus continetur solidis, intercedente      
  28 materia quadam elastica ceu vinculo unitis. Particulae elementares,      
  29 hac intermista, quamvis a contactu mutuo remotae, tamen huius ope semet      
  30 attrahunt et artius profecto colligantur, quam per contactum immediatum fieri      
  31 posset. Quippe contactus molecularum ut plurimum globosarum, cum vix      
  32 puncto fiat, infinities debilior foret ea, quae per universam praestatur superficiem,      
  33 cohaesione. Hac vero ratione situs elementorum mutari salva cohaesione      
  34 potest et simul in promptu est, quomodo, detracta ex interstitiis ex parte materia      
  35 illa uniente, propius sibi possint elementa accedere et volumen contrahere;      
  36 contra ea, aucta vel quantitate vel etiam elasticitate ipsius, corpus volumine      
  37 augescere et particulae a se invicem recedere absque cohaesionis iactura      
  38 possint. Quae in theoria ignis maximi momenti sunt.      
           
           
     

[ Seite 374 ] [ Seite 376 ] [ Inhaltsverzeichnis ]