Kant: AA XIV, Mathematik , Seite 005
Zeile:
Text:
[ Seite 004 ] [ Seite 006 ] [ Inhaltsverzeichnis ]
Kant: AA XIV, Mathematik , Seite 005 |
|||||||
Zeile:
|
Text:
|
|
|
||||
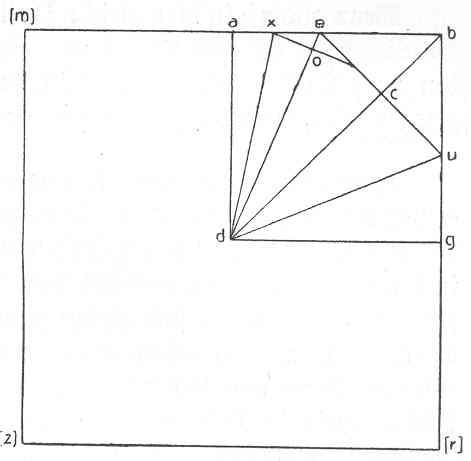
| 01 | (g ae = ec |  | |||||
| 02 | ec:eb = ad:db | ||||||
| 03 | db:ad = eb:ec | ||||||
| 04 | oe:xe = ae:ed | ||||||
| 05 | ax = xo | ||||||
| 06 | xo:xe = ad:de | ||||||
| 07 | ax:xe = ad:de | ||||||
| 08 | ab:ec = db:ad | ||||||
| 09 | ax.eb:xe.ec = db:de ) | ||||||
| 10 | weil ae = cb ∠ ceb | ||||||
| 11 | ∠ ceb = ∠ dba, ergo | ||||||
| 12 | (ec = cb) | (g ec:eb = ad:db | |||||
| 13 | nun ist cb:eb = ab:db | sed ec = ae. Ergo | |||||
| 14 | (also ec:eb = ab:db ) | ae:eb = ad:db | |||||
| 15 | wenn also ec = ae so ist | ( = 1:√2 | |||||
| 16 | wenn nun ae eb = ae so ist | ae2:eb2 = 1:2 ) | |||||
| 17 | ec:ae = ab:db . | ad = ab | |||||
| 18 | soll also ec = ae werden | Ergoab:ae = db:eb | |||||
| 19 | oder vielmehr au = uo | also ae:eb = ab:db ) | |||||
| 20 | (ab - eb) (= ae) (= ec) = cb | ||||||
| 21 | also (ab - eb):eb = ab:db | ||||||
| 22 | aber ec = cb, mithin (ab - eb) = cb | ||||||
| 23 | also cb:eb = ab:db | ||||||
| 24 | und cb = ec = ae | ||||||
| 25 | also ae:eb = ab:db | | (g ax:xe = R:√(2R2) ) | |||||
| 26 | ab:db = 1:√2 | ||||||
| 27 | also ae:eb = 1:√2 | ||||||
| [ Seite 004 ] [ Seite 006 ] [ Inhaltsverzeichnis ] |
|||||||