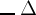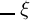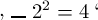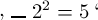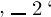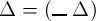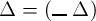Seite 9
§ 5.
Schon oben ist gesagt, dass in der blossen Gleichung noch gar
keine Behauptung liegen soll; es ist mit ‚2+3=5‘ eben nur
ein Wahrheitswerth bezeichnet, ohne dass gesagt ist, welcher von
beiden es ist. Auch wenn ich schriebe ‚(2+3=5)=(2=2)‘
und voraussetzte, man wüsste, dass 2=2 das Wahre
ist, so würde ich doch damit nicht behauptet haben, dass die
Summe von 2 und 3 5 ist, sondern
ich hätte nur den Wahrheitswerth davon bezeichnet, dass
‚2+3=5‘ dasselbe bedeute wie 2=2. Wir bedürfen
also noch eines besonderen Zeichens, um etwas als wahr behaupten
zu können. Zu diesem Zwecke lasse ich dem Namen des
Wahrheitswerthes das Zeichen ‚⊦‘
vorhergehen, so dass z. B. in
behauptet wird, dass das Quadrat von 2 4 sei. Ich
unterscheide das Urtheil vom
Gedanken in der Weise, dass ich
unter Urtheil die Anerkennung der
Wahrheit eines Gedankens verstehe.
Die begriffsschriftliche Darstellung eines Urtheils mittelst des
Zeichens ‚⊦‘ nenne ich Begriffsschriftsatz oder kurz Satz. Dieses ‚⊦‘
sehe ich an als zusammengesetzt aus dem senkrechten Striche, den
ich Urtheilstrich nenne, und dem
wagerechten, den ich jetzt einfach den Wagerechten nennen will.
Der Wagerechte wird meist mit andern Zeichen, wie hier mit dem
Urtheilstriche verwachsen vorkommen und dadurch vor der
Verwechselung mit dem Minuszeichen geschützt sein. Da, wo er
gesondert vorkommt, muss er zur Unterscheidung etwas länger als
das Minuszeichen gemacht werden.
Ich fasse ihn als Functionsnamen auf in der Weise, dass
das Wahre ist, wenn Δ das
Wahre ist, dass es dagegen das Falsche ist, wenn Δ nicht das Wahre ist.
Demnach ist
eine Function, deren Werth immer ein Wahrheitswerth ist,
oder nach
Seite 10
unserer Festsetzung ein Begriff. Unter diesen Begriff fällt das
Wahre und nur dieses. Es bedeutet also
dasselbe wie ‚22=4‘, nämlich das Wahre. Um Klammern
entbehrlich zu machen, bestimme ich nämlich, dass Alles, was
rechts vom Wagerechten steht, als Ganzes aufzufassen ist, das an
der Argumentstelle der Function —ξ
steht, sofern nicht Klammern das
verbieten. Es bedeutet
das Falsche, also dasselbe wie ‚22=5‘, wohingegen
das Falsche bedeutet, also etwas von der Zahl
2 Verschiedenes. Wenn Δ ein Wahrheitswerth ist, so ist —Δ derselbe und mithin ist dann
das Wahre. Es ist dies aber das Falsche, wenn
Δ kein Wahrheitswerth ist. Wir
können also sagen, dass
der Wahrheitswerth davon ist, dass Δ ein Wahrheitswerth sei. Die Function —Φ(ξ) ist danach ein Begriff, und die Function
—Ψ(ξ, ζ) ist eine Beziehung,
einerlei, ob Φ(ξ) ein Begriff und
Ψ(ξ, ζ) eine Beziehung ist oder
nicht. Von den beiden Zeichen, aus
denen ‚⊦‘ zusammengesetzt ist,
enthält nur der Urtheilstrich die Behauptung.
1 Ich benutze hier vielfach die
Bezeichnungen der Summe, des Products, der Potenz vorläufig,
obwohl sie hier noch nicht definirt sind, um bequemer Beispiele
bilden zu können und durch Winke das Verständniss zu erleichtern.
Es muss aber im Auge behalten werden, dass nichts auf die
Bedeutungen dieser Bezeichnungen gegründet wird.
2 Früher nannte ich ihn Inhaltsstrich, als ich noch unter dem Ausdrucke
‚beurtheilbarer Inhalt‘ das zusammenfasste, was ich nun
unterscheiden gelernt habe als Wahrheitswerth und Gedanken.
Vergl. meinen Aufsatz Ueber Sinn und Bedeutung.
3 Selbstverständlich darf das Zeichen
‚Δ‘ nicht bedeutungslos sein,
sondern muss einen Gegenstand bedeuten. Bedeutungslose Namen
dürfen in der Begriffsschrift nicht vorkommen. Die Festsetzung
ist so getroffen, dass ‚—Δ‘ unter
allen Umständen etwas bedeutet, sofern nur ‚Δ‘ etwas bedeutet. Sonst würde —ξ kein scharfbegrenzter Begriff, also in
unserm Sinne überhaupt kein Begriff sein. Ich gebrauche hier die
grossen griechischen Buchstaben als
Namen so, als ob sie etwas bedeuteten, ohne dass ich die
Bedeutung angebe. In den Begriffsschriftentwickelungen selbst
werden sie ebenso wenig wie ‚ξ‘ und
‚ζ‘ vorkommen.
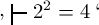 1
1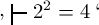 1
1